**sphericity In Repeated Measures**

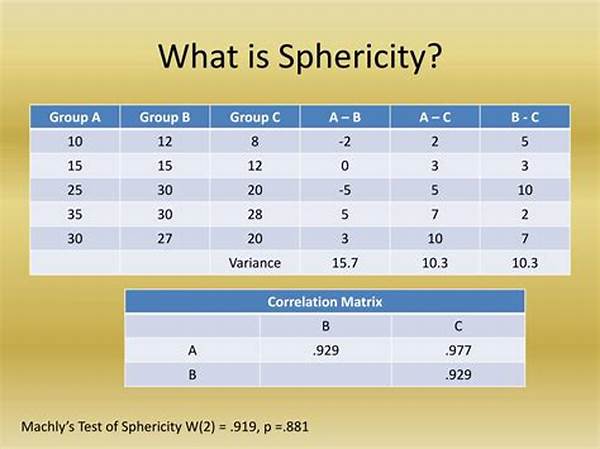
Introduction to Sphericity in Repeated Measures

Sphericity in repeated measures is a crucial assumption in statistical analyses that involve repeated measures designs, often encountered in fields such as psychology, medicine, and social sciences. This assumption pertains to the equality of variances of the differences between all possible pairs of within-subject conditions. When sphericity is violated, it can lead to inaccurate statistical inferences, such as inflated Type I error rates. Ensuring sphericity is satisfied is essential for the proper application of ANOVA techniques in repeated measures, where each participant is exposed to multiple conditions or time points.

Read Now : Cultivating Moral Values In Research

The concept of sphericity is integral to maintaining the validity of the statistical tests conducted under repeated measures frameworks. It arises because repeated measures designs involve correlated observations, and the assumption of sphericity helps in maintaining the homogeneity of these correlations. Failure to address sphericity in repeated measures may lead to biases in hypothesis testing outcomes. This highlights the need for researchers to test for sphericity and apply necessary corrections, such as adjustments provided by Greenhouse-Geisser or Huynh-Feldt, when this assumption is not met.

Detecting departures from sphericity in repeated measures is typically done using Mauchly’s Test of Sphericity. If sphericity is violated, as often indicated by this test, alternative statistical methods or corrections are employed. Adhering to the sphericity assumption ensures that conclusions drawn from the data are reliable, preserving the scientific integrity of the research findings. Understanding and addressing sphericity issues can significantly enhance the robustness of analyses carried out in repeated measures designs.

Addressing Violations of Sphericity in Repeated Measures

1. Mauchly’s Test of Sphericity: A widely used procedure to test for sphericity in repeated measures, Mauchly’s test evaluates whether the covariance matrix of the differences is proportional to an identity matrix. If this test yields a significant result, the assumption of sphericity is violated.

2. Greenhouse-Geisser Correction: When violations of sphericity in repeated measures are detected, the Greenhouse-Geisser epsilon provides a correction factor to adjust the degrees of freedom for the F-test, thereby mitigating the impact of sphericity violations on statistical outcomes.

3. Huynh-Feldt Correction: An alternative to the Greenhouse-Geisser correction, the Huynh-Feldt correction also provides an epsilon that adjusts the degrees of freedom in cases where sphericity in repeated measures is not met, offering a less conservative adjustment.

4. Multivariate Approach: In some instances, researchers may opt for a multivariate analysis approach as a remedy for sphericity violations. This approach does not assume sphericity and can be advantageous when dealing with severe violations of this assumption.

5. Data Transformation Techniques: Transforming the data can sometimes address violations of sphericity in repeated measures. Techniques such as logarithmic transformation may stabilize variance and make the data meet the sphericity requirement more closely.

Implications of Sphericity in Repeated Measures Analysis

The implications of sphericity in repeated measures analysis are profound, influencing both the design and interpretation of statistical tests in a significant way. When researchers neglect to account for sphericity, the risk of drawing erroneous conclusions increases due to potential violations of the required statistical assumptions. This underscores the necessity of comprehensive testing and correction for sphericity in repeated measures to preserve the reliability of the results.

Sphericity in repeated measures is particularly relevant when analyzing data involving multiple time points or conditions for the same subjects. The intricate nature of repeated measures designs entails that observations are inherently correlated, a factor which the sphericity assumption seeks to manage appropriately. Ensuring adherence to this assumption through tests or corrective measures helps maintain the precision of hypothesis testing, thus providing credible, empirical results that can be utilized for informed decision-making in various fields of study.

Practical Considerations in Handling Sphericity in Repeated Measures

1. Conduct Pre-Testing: Before running an ANOVA, assess the data for sphericity to decide if adjustments are needed.

2. Use Epsilon Adjustments: Familiarize yourself with epsilon values from Greenhouse-Geisser and Huynh-Feldt techniques for accurate df adjustment.

3. Explore Non-Parametric Tests: Consider non-parametric alternatives if transformations or adjustments are insufficient.

4. Adopt Mixed Models: Mixed-effects models offer flexibility and are less sensitive to sphericity violations.

Read Now : Verifying Academic Reference Sources

5. Report Findings Transparently: Clearly document methods used to check and correct sphericity issues when reporting results.

6. Account for Sample Size: Larger sample sizes increase the likelihood of detecting significant results even when corrections are applied.

7. Review Correlations: Check within-subject correlations to understand the extent of sphericity violations.

8. Reassess Model Fit: Ensure that the chosen model appropriately fits the data by examining residuals and other diagnostic measures.

9. Implement Software Tools: Utilize statistical software tools that can automate the process of testing and correcting for sphericity.

10. Train in Advanced Methods: Ensure team members are trained in advanced statistical methods relevant to handling sphericity.

Strategies to Manage Sphericity in Repeated Measures Studies

Managing issues related to sphericity in repeated measures studies involves several strategic approaches. First and foremost, conducting preliminary analyses to gauge the presence of sphericity is essential. This involves applying Mauchly’s Test of Sphericity to identify any potential violations. When violations are found, adopting correction methods such as Greenhouse-Geisser or Huynh-Feldt becomes imperative to adjust the degrees of freedom appropriately.

Additionally, researchers should consider the benefits of employing mixed-effects models, which offer robust alternatives that are less prone to the effects of sphericity violations in repeated measures. These models allow for the inclusion of random effects and can accommodate more complex data structures, thereby enhancing the quality of statistical inferences. Another viable approach includes non-parametric methods, which do not rely on sphericity assumptions and can be particularly useful when data transformations fail to yield satisfactory results.

Lastly, enhancing research practices through comprehensive training in advanced statistical techniques and ensuring the use of software tools capable of handling complex models is advisable. By equipping themselves with the appropriate skills and resources, researchers can effectively minimize the impact of sphericity violations, thereby ensuring the accuracy and reliability of findings derived from repeated measures studies.

Conclusion on Sphericity in Repeated Measures Analysis

The consideration of sphericity in repeated measures is indispensable for the integrity of statistical analyses in repeated measures designs. As a fundamental assumption, sphericity ensures that the computations of F-tests are valid and that Type I error rates remain controlled. Researchers, therefore, bear the responsibility of testing for and addressing any deviations from sphericity, applying necessary statistical corrections or alternative analytic strategies.

While addressing sphericity in repeated measures may present challenges, it ultimately leads to more reliable and generalizable research findings. The application of corrections such as Greenhouse-Geisser or the utilization of robust alternative models highlights the multifaceted approaches researchers can employ. By prioritizing fidelity to statistical assumptions, scholars ensure the validity of their research contributions and provide a sound basis for subsequent applications or studies within their respective fields.