Hypothesis Testing In Quantitative Research

In the domain of quantitative research, hypothesis testing serves as a pivotal methodological tool. It provides a systematic approach to evaluate the authenticity of scientific assumptions within a defined framework. Through the implementation of hypothesis testing in quantitative research, practitioners can make informed decisions rooted in empirical data, significantly enhancing the validity and reliability of their findings. This article delves into the critical components of hypothesis testing, elucidating its role and application in quantitative research.

Read Now : Integrating Ethics In Classroom Lessons

The Essence of Hypothesis Testing

Hypothesis testing in quantitative research is a significant component that governs the process of scientific inquiry. It is primarily concerned with evaluating the probability that a given hypothesis about a population parameter holds true. This evaluation is achieved through a structured process, typically involving the formulation of null and alternative hypotheses, the selection of a suitable test statistic, and the determination of the statistical significance threshold. The objective is to ascertain whether to accept or reject the initial hypothesis based on empirical evidence. Hypothesis testing in quantitative research empowers researchers to substantiate their claims with precision and analytical rigor.

The credibility of quantitative findings largely hinges on the robust application of hypothesis testing. By employing statistical techniques, researchers are capable of quantifying the likelihood of observing their results, assuming the null hypothesis is accurate. This inferential process is a cornerstone of statistical analysis, as it allows conclusions to be drawn beyond the immediate dataset. Consequently, hypothesis testing facilitates the advancement of knowledge by supporting the establishment of generalized insights and the development of theoretical frameworks. It is imperative in ensuring that conclusions are not merely coincidental or anecdotal but rather scientifically sound and replicable.

Furthermore, hypothesis testing in quantitative research is instrumental in informing practical decision-making. In diverse fields such as psychology, economics, and medicine, the ability to discern true effect from random variation is crucial. Researchers can leverage hypothesis testing to validate new theories, test the efficacy of interventions, and effectuate policy changes based on data-driven evidence. Thus, this methodology not only strengthens the academic body of work but also bridges the gap between research and real-world application, driving innovation and societal progress.

Key Components of Hypothesis Testing

1. Null and Alternative Hypotheses: Building blocks of hypothesis testing in quantitative research, these propositions represent the status quo and the researcher’s theory, respectively. The null hypothesis posits no effect or relationship, while the alternative suggests the contrary.

2. Test Statistic: A numerical summary used in hypothesis testing to determine the likelihood of observing the data under the null hypothesis. It plays a pivotal role in making inferences from the data.

3. P-Value: This measurement gauges the strength of evidence against the null hypothesis. In hypothesis testing in quantitative research, a smaller p-value indicates a stronger presumption against the null hypothesis.

4. Significance Level: Denoted by alpha, this threshold determines the critical value beyond which the null hypothesis is rejected. It embodies the probability of committing a Type I error in hypothesis testing in quantitative research.

5. Type I and Type II Errors: Potential errors in decision-making within hypothesis testing. A Type I error involves incorrectly rejecting a true null hypothesis, while a Type II error pertains to the failure of rejecting a false null hypothesis.

Hypothesis Testing Procedures

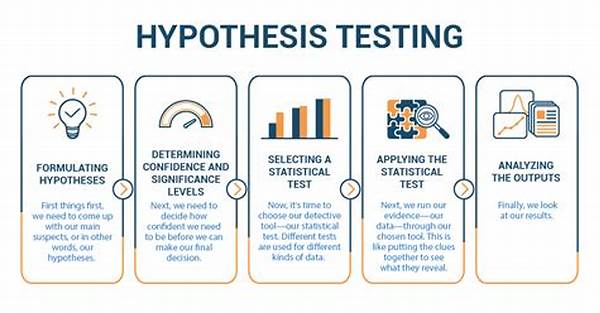
The procedure for hypothesis testing in quantitative research follows a systematic sequence of steps to ensure robust outcomes. Initially, researchers formulate two competing hypotheses: a null and an alternative. This distinction is vital as it provides a framework for comparing observed data against expected outcomes. Thereafter, an appropriate statistical test is selected based on data characteristics, ensuring alignment with the research question and data structure.

Next, a significance level is established, usually set at 0.05 or 5%, to determine the threshold for rejecting the null hypothesis. The chosen test statistic is computed using sample data and compared against critical values derived from statistical theory. This comparison yields a p-value, which guides the acceptance or rejection of the null hypothesis. A p-value lower than the significance level indicates that the null hypothesis can be rejected with a high degree of confidence.

This methodical approach ensures that hypothesis testing in quantitative research maintains scientific rigor and objectivity. By adhering to these established procedures, researchers can confidently translate empirical evidence into validated findings, contributing to the overarching goals of scientific exploration and discovery.

Advantages and Limitations

Hypothesis testing in quantitative research offers several advantages, including a structured approach to data analysis and decision-making. It provides a mechanism to quantify uncertainties and assess the reliability of results, ensuring that conclusions are supported by a rigorous statistical foundation. Additionally, its ability to generalize findings enhances the applicability of research across different contexts and populations.

However, hypothesis testing also has limitations. It is contingent upon the assumption of a normal distribution, which may not be met in all datasets, potentially affecting the accuracy of conclusions. The reliance on arbitrary significance levels, typically set at 0.05, has been criticized for oversimplifying the complexity of real-world data. Moreover, hypothesis testing focuses primarily on statistical significance, which does not necessarily equate to practical significance.

Read Now : Concise Writing For Academic Abstracts

Despite these limitations, hypothesis testing remains indispensable in the quantitative research paradigm. Researchers are encouraged to complement this technique with other statistical methods and subject-matter expertise to achieve comprehensive and meaningful insights.

Practical Applications in Various Fields

Hypothesis testing in quantitative research finds vast applications across diverse scientific disciplines. In the domain of psychology, it is employed to evaluate behavioral theories and cognitive processes, enabling the identification of causal relationships and validation of experimental treatments. Economists utilize hypothesis testing to analyze financial trends and forecast market behaviors, providing insights essential for economic planning and policy formulation.

In the medical field, hypothesis testing is crucial for clinical trials, assessing the efficacy and safety of new treatments and drugs before they are made available to the public. Environmental scientists leverage it to understand ecosystem changes and the impact of human activities, driving conservation efforts and sustainable practices. Furthermore, in education, hypothesis testing aids in the evaluation of teaching methods, curriculum effectiveness, and student performance metrics.

Hypothesis testing in quantitative research serves as a cornerstone in scientific investigation, offering a robust framework for evidence-based findings and promoting continual advancements in various fields. It underscores the importance of statistical literacy and rigorous analytical skills in contributing to the body of knowledge.

Nuances of Null Hypothesis

1. The null hypothesis, denoted as H0, presupposes no effect or relationship in the study.

2. It acts as a refutable stand-in theory, pivotal in hypothesis testing in quantitative research.

3. A rejected null hypothesis suggests the presence of a significant effect or relationship.

4. The formulation of the null hypothesis demands clarity and precision.

5. Acceptance of H0 implies the outcomes are attributed to chance variations.

Conclusion and Future Directions

In conclusion, hypothesis testing in quantitative research stands as an indispensable element of empirical investigation, guiding the verification and falsification of scientific theories. It ensures that research findings are not only statistically significant but also theoretically sound, providing a solid foundation for advancing knowledge and informing practice. Despite the intrinsic limitations associated with its application, hypothesis testing remains an integral part of the scientific endeavor, fostering a rigorous understanding of complex phenomena.

Looking forward, there is a growing impetus to enhance hypothesis testing methodologies to address contemporary challenges, such as the reproducibility crisis and the need for more nuanced interpretations of data. By integrating complementary statistical techniques and fostering interdisciplinary collaborations, researchers can refine their analytical approaches, ensuring that hypothesis testing continues to evolve in line within the dynamic landscape of quantitative research. Furthermore, innovations in computational capabilities and data analytic tools promise to extend the scope and depth of hypothesis testing, making it an even more powerful tool for unlocking scientific insights.