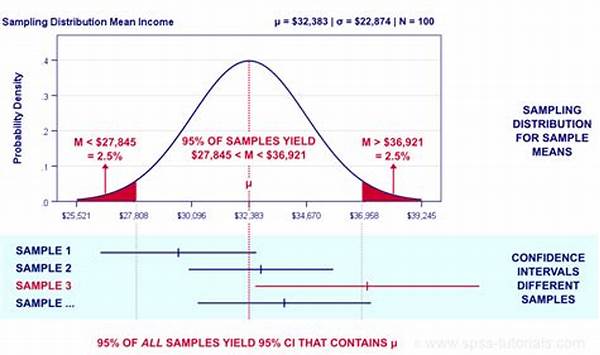
Confidence Intervals For Sampling

Confidence intervals are a fundamental component in statistical analysis, providing a range within which we expect a population parameter to lie based on sample data. This article delves into the depths of confidence intervals for sampling, emphasizing their importance and application in statistical inference.

Read Now : Citation Tools For Academic Success

Understanding Confidence Intervals for Sampling

Confidence intervals for sampling serve as an essential tool for statisticians when estimating population parameters. They offer a calculated range of values that, with a certain level of confidence, likely contain the true population parameter. This concept is crucial because it acknowledges the inherent uncertainty present in sampling. By constructing confidence intervals, researchers can express this uncertainty quantitatively, thereby facilitating more informed decision-making based on sample data.

The determination of a confidence interval involves specifying a confidence level, commonly set at 95% or 99%, and calculating the range using the sample mean and standard deviation. These intervals not only convey a statistical estimate but also allow researchers to account for variability by expressing the potential margin of error. Consequently, confidence intervals are instrumental in drawing conclusions about a population without having to conduct a full census.

Moreover, confidence intervals for sampling are particularly valuable in hypothesis testing. By assessing whether a hypothesized parameter value falls within a calculated interval, statisticians can determine the plausibility of their hypotheses. This utility extends across diverse fields, including public health, economics, and the social sciences, where sampling is often more practical than surveying entire populations. Thus, understanding and appropriately applying confidence intervals for sampling is a critical skill for professionals engaged in data analysis and interpretation.

Factors Influencing Confidence Intervals for Sampling

1. Sample Size: The size of the sample plays a pivotal role in determining the width of confidence intervals for sampling. Larger samples tend to produce narrower intervals, reflecting greater precision in estimating the population parameter.

2. Confidence Level: The confidence level chosen affects the interval width. Higher confidence levels, such as 99%, result in broader intervals compared to lower levels like 90%, indicating a trade-off between certainty and precision.

3. Population Variability: Greater variability within a population often leads to wider confidence intervals for sampling. This is because high variability introduces more uncertainty in estimating the mean or proportion.

4. Data Distribution: The shape of the data distribution influences the construction of confidence intervals. While normal distribution is often assumed, deviations from normality require adjustments in interval calculation through techniques such as bootstrapping.

5. Estimation Method: The method of estimation, whether for means or proportions, affects the formula and assumptions used in calculating confidence intervals for sampling. Different parameter types necessitate specific approaches to interval estimation.

Constructing Confidence Intervals for Sampling

Confidence intervals for sampling are typically constructed following a systematic process. Initially, researchers must select an appropriate confidence level, often dictated by the study’s goals and the degree of certainty required. This level represents the probability, expressed as a percentage, that the interval will contain the true population parameter based on repeated sampling. Following this, data collection occurs, with careful attention to ensure random sampling to minimize biases that could compromise the interval’s accuracy.

To calculate the interval, researchers first determine the sample mean and standard error. These metrics are critical in forming the foundation upon which the interval is built. The formula incorporates the chosen confidence level’s corresponding critical value, which reflects the point on the standard normal distribution that will include the specified proportion of data. This mixture of sample statistics and theoretical values yields the interval, which provides insight into potential parameter ranges, informed by the sample data.

Confidence intervals for sampling not only furnish estimates but also impart a degree of reliability to statistical conclusions. By defining the probable range for a parameter, they facilitate contextual understanding of data analysis results. This clarity is indispensable in applied research, where decision-makers must rely on statistical evidence to guide policies and strategies. Consequently, mastering the construction of confidence intervals is a vital competency in empirical research across various disciplines.

Applications of Confidence Intervals for Sampling

Confidence intervals for sampling find applications across numerous domains:

1. Healthcare Research: In clinical trials, confidence intervals help evaluate the efficacy of treatments by estimating potential differences in outcome measures between control and experimental groups.

2. Social Sciences: Researchers employ confidence intervals to assess public opinion and behavioral trends through surveys, reflecting the extent of population agreement with various topics.

3. Economics: Economists use confidence intervals for sampling when predicting economic indicators like gross domestic product, providing an uncertainty range in forecasts.

4. Quality Control: Manufacturing processes utilize confidence intervals to ensure products meet quality standards by estimating defect percentages within production batches.

5. Agricultural Studies: Agronomists apply confidence intervals to quantify yield differences across crop varieties under differing conditions, promoting informed agricultural practices.

6. Psychological Research: Studies on mental health and behavior utilize confidence intervals to generalize findings from samples to populations, enhancing the impact of research conclusions.

7. Political Polling: During elections, confidence intervals are crucial in interpreting poll results, suggesting potential election outcomes within specified confidence levels.

8. Environmental Science: Environmental assessments use confidence intervals to measure pollutant levels, aiding in regulatory compliance and conservation efforts.

Read Now : Encouraging A Growth Mindset

9. Educational Testing: Confidence intervals are applied in standardizing test scores to ensure fair comparisons of student performance across different demographics.

10. Marketing Research: Businesses leverage confidence intervals to estimate market share and consumer preferences, guiding strategic marketing decisions.

The Importance of Confidence Intervals for Sampling in Research

Confidence intervals for sampling are integral to validating research findings, ensuring that conclusions drawn are not mere artifacts of sample variation. Within the scientific community, robustness in inference strengthens the integrity of research, and confidence intervals play a central role in achieving this objective. By providing a probabilistic framework through which researchers can interpret sample data, confidence intervals offer a powerful means of conveying uncertainty—an essential aspect of rigorous scientific inquiry.

In practice, confidence intervals contribute significantly to enhancing the reproducibility of studies, as they furnish transparency in estimation procedures. This transparency not only fosters collaboration and trust among researchers but also aids in the evaluation of methodologies applied to diverse datasets. When confidence intervals are communicated in published research, they allow practitioners across disciplines to better assimilate and apply research findings to real-world contexts, facilitating the translation of data into actionable insights.

The implementation of confidence intervals for sampling reflects a commitment to methodological rigor and precision. As research increasingly informs policy decisions and practical applications, the need for accurate and reliable statistical tools becomes paramount. Confidence intervals serve not only to bolster the credibility of research but also to bridge the gap between empirical findings and their broader implications, thus contributing to the scientific advancement and societal progress.

Challenges in Interpreting Confidence Intervals for Sampling

Understanding confidence intervals for sampling is not without challenges. Researchers must navigate these potential pitfalls to draw valid inferences:

1. Misinterpretation of Confidence Levels: Confidence levels are often incorrectly interpreted as the probability that the interval contains the true parameter, which could lead to misconceptions about statistical certainty.

2. Overreliance on Sample Data: Reliance on sample data may introduce bias, particularly if sampling is not random, thus affecting the interval’s validity and representativeness for the population.

3. Ignoring Assumptions: Confidence intervals rely on assumptions regarding data distribution; overlooking these assumptions can result in inaccurate estimates that misguide conclusions.

4. Sample Size Considerations: Small sample sizes can lead to wide confidence intervals, diminishing the estimate’s precision and making it difficult to draw meaningful inferences.

5. Complexity of Non-Normal Data: When data deviate significantly from a normal distribution, traditional methods for constructing confidence intervals may not be appropriate, necessitating more sophisticated techniques.

6. Lack of Contextual Understanding: Without context, confidence intervals are mere numerical estimations; understanding their implications requires comprehensive knowledge of the subject matter.

7. Fluctuating Interval Widths: Variations in interval widths, influenced by study design or data anomalies, can complicate comparisons across different datasets or research settings.

8. Overconfidence in Results: Excessive confidence in narrow intervals might overlook the potential impact of unaccounted variables, leading to exaggerated claims about a study’s findings.

9. Difficulty in Communication: Articulating the meaning and significance of confidence intervals to non-statistical audiences poses challenges in effectively conveying the uncertainty involved.

10. Balancing Precision and Certainty: Researchers must weigh the trade-off between narrower intervals with low confidence levels and broader intervals that provide higher certainty.

Conclusion on Confidence Intervals for Sampling

In conclusion, confidence intervals for sampling are a cornerstone of statistical analysis, offering a bridge between raw data and meaningful insights. These intervals encapsulate the precision associated with parameter estimation, enabling researchers to express findings with a warranted degree of certainty. As society increasingly relies on data-driven decision-making, confidence intervals’ role in shaping conclusions becomes ever more critical. Researchers must continue to advance their understanding and application of these statistical constructs to uphold the integrity of their work and support informed judgments in various domains. By doing so, they ensure that data not only illuminates current phenomena but also provides a reliable foundation for future inquiry and exploration.